Takeaway

I tassi di interesse sono lo strumento utilizzato per confrontare pagamenti che avvengono in momenti diversi nel tempo. Il concetto centrale è quello di present value, che permette di esprimere un cash flow futuro in termini di valore attuale attraverso una relazione formale basata, per l’appunto, sul tasso di interesse.

Il problema del confronto nel tempo

Spesso nei mercati finanziari, diviene necessario confrontare pagamenti che avvengono in momenti diversi. Per affrontare tale problema partiremo dal porre un quesito: Vale più un euro oggi o un euro domani?

Bene, un euro oggi non è equivalente a un euro ricevuto in futuro, perché l’ euro disponibile oggi può essere investito e generare un rendimento. Ora per capire il perché, è necessario disporre di uno strumento che permetta di confrontare valori monetari collocati in periodi diversi.

Per rendere confrontabili pagamenti futuri con valori presenti, gli economisti utilizzano il concetto di present value (PV).

Come abbiamo già accennato sopra, il concetto di present value si basa sull’assunto che un euro ricevuto tra un anno vale meno di un euro ricevuto oggi, proprio perché ne puoi subito fare un uso fruttuoso e ricavarne un interesse.

Partiamo da un semplice esempio. Immaginiamo di fare un prestito di 1000 euro a Francesca, che dovrà ripagarti in un anno con un interesse, di 100 euro In questo caso, trattandosi di un interesse semplice i avremo:

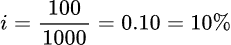
In sostanza effettuando un prestito a francesca di 1000 euro alla fine dell’anno otterresti 1100 euro :

1000 x ( 1 + 0.10) = 1100 euro

Seguendo tale metodo se avessimo effettuato lo stesso prestito da restituire in 3 anni otterremmo:

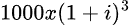
ovvero 1331 euro .

Allora, cosa ci dice questo semplice esempio?

Beh essenzialmente che possiamo vedere tale prestito partendo dal futuro e tornando indietro al presente. Quindi continuando con il nostro esempio:

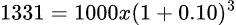
a tre anni da ora, valgono 1000 euro oggi :

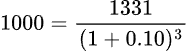
In soldoni, il processo di calcolare il valore attuale di 1 euro ricevuto in futuro è detto discounting the future o attualizzare i flussi di cassa futuri.

in termini generali :

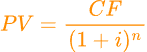
In questo senso il concetto di present value (valore attuale), risulta estremamente utile, perché, dato un certo tasso di interesse semplice, consente di capire il prezzo attuale di uno strumento di debito/credito di mercato aggiungendo i valori attuali dei singoli pagamenti futuri ricevuti. Ciò consente di paragonare due o più strumenti che hanno differenti tempistiche nei pagamenti.

Definizione di Yield to Maturity

Lo yield to maturity (YTM) in italiano tasso di rendimento effettivo a scadenza (TRES) è definito come:

Tasso di rendimento che consente di eguagliare, in senso finanziario, il prezzo pagato per acquistare un titolo di debito con la somma dei valori attuali di tutti i flussi futuri, sia in linea interessi che in linea capitale, che maturano a beneficio del possessore.

In altre parole, il punto chiave per calcolare lo YTM è che eguaglia il prezzo corrente di un’obbligazione al valore attuale dei suoi pagamenti futuri.

Come si calcola lo YTM su un prestito personale ?

Dominic prende a prestito 1000 euro dalla sorella, dovendole restituire dopo 1 anno 1100 euro. In questo caso lo YTM sarà pari al 10% ovvero:

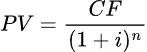
con PV pari a 1000 euro, CF pari a 1100 euro ovvero il flusso di cassa passato un anno, n il numero degli anni,

Quindi:

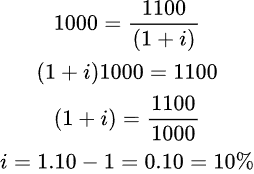
Come si può notare per ciò che concerne un semplice prestito il tasso di interesse semplice è uguale allo YTM.

Come si calcola lo YTM su un mutuo a tasso fisso?

Partiamo da un prestito di 1000 euro e i pagamenti annuali sono pari a 136 euro per 25 anni, seguendo la stessa logica di prima otterremo:

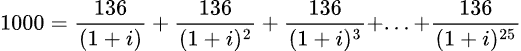
in generale dato che un mutuo a tasso fisso prevede più di un pagamento il valore attuale (PV) di questo tipo di mutuo è calcolato come la somma dei valori attuali dei vari pagamenti, ovvero:

ove LV sta per loan value, FP fixed yearly payment (il pagamento fisso da effettuare ogni anno) e n il numero degli anni alla scadenza.

Approssimativamente lo YTM risolvendo l’equazione di cui sopra è circa il 13%.

Ovviamente le banche utilizzano software/ calcolatrici finanziare per risolvere calcoli così complessi e lunghi, in modo da poter dire all’ acquirente di una casa quanto dovrà pagare come rata annualmente/mensilmente.

Come si calcola lo Ytm Se parliamo di Bond ?

Essenzialmente il concetto é sempre lo stesso, ovvero seguire la strategia utilizzata in precedenza. Prendiamo ad esempio un obbligazione con valore facciale/ nominale ( face value ) di 1000 euro con scadenza a 10 anni e cedole pari a 100 euro ( tasso cedolare 10%):

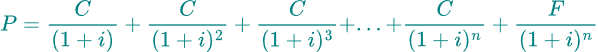
P = prezzo del obbligazione, C = cedola, F = face value (valore nominale), n = numero anni alla scadenza (maturity)

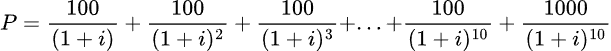
Anche in questo caso i calcoli sono complessi, quindi potete utilizzare software finanziari e calcolatori finanziari per calcolare lo YTM ;)

Tassi di interesse e rendimenti

Nel proseguire l’analisi dei tassi di interesse, gli economisti introducono una distinzione fondamentale tra tasso di interesse e tasso di rendimento (rate of return).
Questa distinzione diventa rilevante quando il prezzo di un’attività finanziaria può variare nel tempo, come accade per le obbligazioni negoziate sul mercato.

Il punto centrale è che il rendimento effettivamente ottenuto da un investimento può differire dal tasso di interesse promesso.

In sostanza gli investitori potrebbero pensare che l’interesse pagato d auna obbligazione sia ciò a cui guardare per capire quale sarà il guadagno ottenuto, ma come stiamo per scoprire non è così.

In generale il rendimento effettivo è il rendimento complessivo ottenuto da un’attività finanziaria in un determinato periodo, tenendo conto sia dei pagamenti ricevuti sia della variazione del prezzo dell’attività stessa, espresso come frazione del prezzo di acquisto.

Facendo un esempio, per calcolare il tasso di rendimento, prendiamo un obbligazione con valore nominale 1000 euro, cedola del 10% , tenuto per un anno e rivenduto a 1200 euro dopo averlo comprato a 1000 euro. Il pagamento cedolare è pari a 100 euro, mente la variazione di prezzo dell’obbligazione è pari a 200 euro, quindi

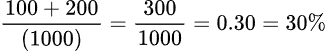
Come si può notare il rendimento effettivo è pari al 30% mentre inizialmente lo YTM era pari al 10%. Questo esempio serve per dimostrare che il tasso di rendimento ottenuto non necessariamente è uguale allo yield to maturity o TRES.

Piu in generale il rendimento di un bond mantenuto da t a t+1 può essere calcolato come:

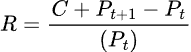
dove R indica il rendimento ottenuto mantenendo l’obbligazione da t a t+1, C è la cedola, P_t è il prezzo dell’obbligazione al tempo t e P_t+1 è il prezzo dell’obbligazione in t+1.

(Per approfondire la tematica obbligazioni https://mfeniellofmj.com/2023/11/16/obbligazioni-e-i-principali-rischi/ e https://mfeniellofmj.com/2023/12/19/obbligazioni-e-i-principali-rischi-ii-la-duration/)

Ora se ci concentriamo sulla seconda parte dell’equazione ovvero :

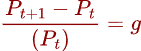
questa rappresenta il tasso di capital gain o meglio il cambiamento nel prezzo dell’obbligazione rispetto al suo prezzo iniziale.

Cosa possiamo dedurre da ciò?

Beh essenzialmente che il rendimento può essere molto diverso dal tasso cedolare se il prezzo dell’obbligazione dovesse subire fluttuazioni tali da poter causare guadagni o perdite. Se ne può dedurre che che le uniche obbligazioni il cui rendimento è uguale al YTM o TRES sono quelle in cui il time to maturity (scadenza) è uguale al periodo di detenzione, e che un aumento sostanziale dei tassi di interesse associato ad un crollo nel prezzo si traduce in perdita per obbligazioni dove a scadenza è più lunga del periodo di detenzione.

In soldoni, appurato che i prezzi delle obbligazioni caratterizzate da scadenze più lunghe si muovono in maniera più rilevante in risposta a cambiamenti nei tassi di interesse, si può affermare che prezzi e rendimenti di obbligazioni a lunga scadenza sono più volatili rispetto a quelli di obbligazioni a breve scadenza.

Ora ci avviamo alla conclusione della nostra trattazione rispondendo ad una domanda fondamentale:

Qual é la differenza tra interessi reali e nominali?

In pratica una distinzione importante da fare è quella tra tasso nominale e tasso di interesse reale, ove quest’ultimo è il tasso aggiustato per l’inflazione cioè, il tasso che si ottiene sottraendo le attese sui sui cambiamenti nel livello dei prezzi, risultando cosi più accurato perché ci racconta l’effettivo costo del prendere a prestito.

Procediamo con ordine: Il tasso di interesse reale ex ante stima il potere d’acquisto futuro di un investimento, basandosi su un’inflazione attesa ( ed è questo al quale gli economisti fanno riferimento parlando di tassi di interesse reali), mentre il tasso di interesse reale ex post calcola il rendimento effettivo dopo che l’inflazione reale si è verificata, mostrando il vero guadagno (o perdita) in termini di potere d’acquisto, e quindi ci dice quanto effettivamente come è andata per che presta, “after the fact“.

Per definire i tassi di interesse reale si utilizza l’equazione di fisher la quale afferma che:

il tasso di interesse nominale i è uguale al tasso di interesse reale r a cui va sommata l’inflazione attesa

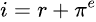
e quindi il tasso di interesse reale è :

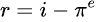
Passando ad un esempio concentro, immaginiamo che il tasso di interesse nominale sia pari al 8% e che l’inflazione attesa sia del 10%, a questo punto quale sarebbe il tasso di interessereale?

Semplicemente basandoci sulla seconda equazione il tasso di interesse reale sarebbe pari a -2%.

E’ facile comprendere che saremo molto meno inclini a prestare denaro, in questo caso, perché in termini di beni reali e servizi ci prendiamo un -2% di interesse. Viceversa se siamo noi a prendere a prestito, andremo bene perché alla fine dell’anno ripagheremo un ammontare che vale il 2% in meno in termini di potere d’acquisto di beni e servizi.

Da qui potete dedurre perché in un contesto di inflazione alta per uno Stato è più facile ripagare gli interessi sul debito pubblico !

---

Se desideri approfondire le implicazioni di questi scenari sui mercati finanziari o sulla pianificazione dei tuoi investimenti, puoi contattarmi per una consulenza personalizzata tramite www.mfeniellofmj.com

---